What are Op-Amps? – Part 2 (Linear Applications)
In this second part of our series on op-amps, we will look at some useful stuff we can make with them, concentrating on linear applications you might find in books or online. In the third article, we will look at non-linear applications.
Choice of Op-Amps
For 90% of the time, you can substitute an op-amp in the circuit you are using with any that you have. I like to keep only a few types (about six) in stock. I prefer a FET input type such as an LF441 (single) and LF442 (dual) and then an LM324 (quad).
They are all suitable for single or dual supply applications. However, if you have stocks of any other types like LF351 or 741, you can use them in any application where the input signal is much smaller than the supply rail.
Single and Split Power Supplies
When I began using op-amps, I found this confusing and frustrating—I would find a particular circuit I wanted in a book but was put off if it had a dual supply and I wanted to run it off a battery. So here is the way to do it.
Obviously, you could use two 9V batteries and connect them in series, the center point becoming the ground, but this is messy and expensive. A better way is to use a second op-amp and generate a virtual common, as shown in Figure C below.
Op-amps are much cheaper than a second battery, and if you use a package with two or four op-amps, it can be done. Capacitors are cheap, and it is a good idea to be generous with them. I generally use a 47uF parallel with a 0.1uf as close to each power pin as possible and to the ground. But remember not to reverse the 47uF on the -ve pin!
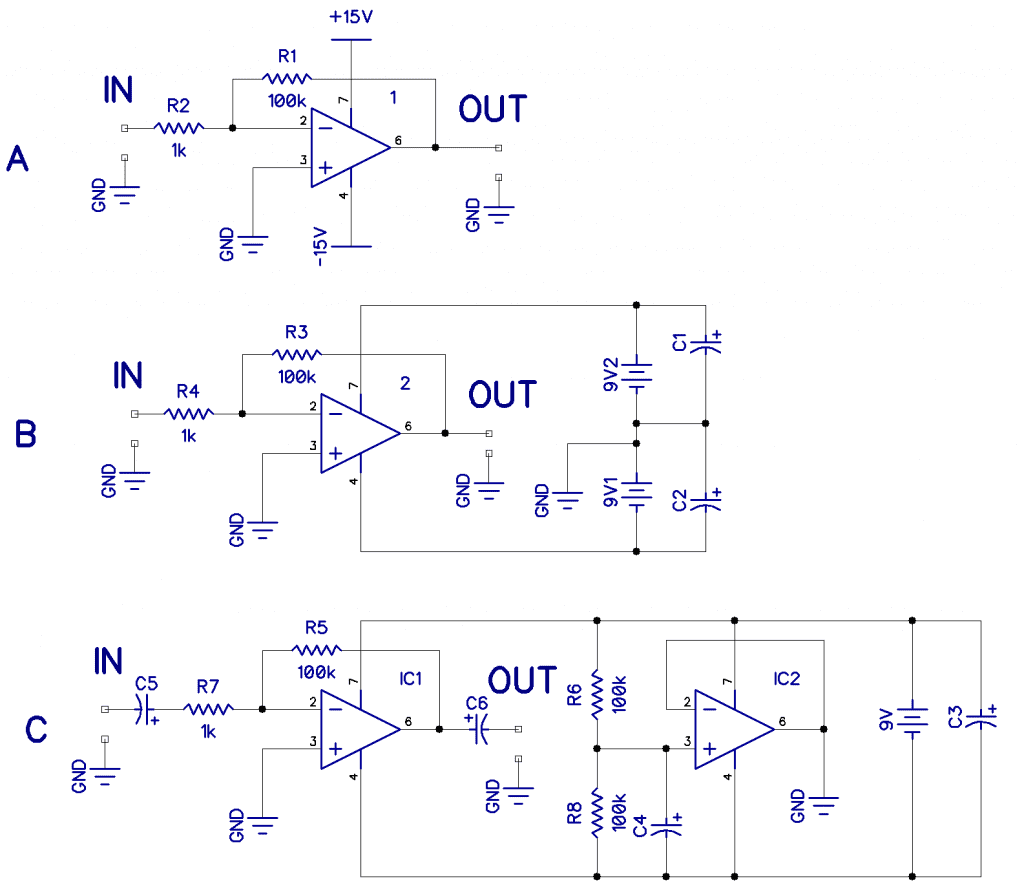
Shown above is an “evolution” of what I am saying.
[A] is the original circuit you might have found in a book, implying a split power supply. In [B], we have put in the two-battery split supply. Note the addition of two decoupling capacitors, C1 and C2 (100uF will do), and the connection of the battery common point to the ground.
One advantage of [A] and [B] is that the input and outputs are almost at ground potential. In [C], we have used a second op-amp to generate the common. At first glance, you might fear that the output of IC2 is ”shorted to ground,” but this is exactly what we wanted to achieve. Although we only have one battery, the input and output points are about 4.5V and need to be isolated with C5 and C6. IC2 works as R6 and R8 form a potential divider forcing the output of IC2 (a voltage follower) to be at half the battery voltage, which is what we want as a virtual common. C4 is essential and is about 100uF.
This might be a good time to discuss coupling capacitors in general. If a circuit is being fed from a low impedance to a high impedance, the choice of series coupling capacitor is governed by the higher impedance (actually, it’s both the low and high in series, but this will only matter if both are high). We choose the capacitor to have the same reactance at the 3dB roll-off point of the lowest frequency we want to pass.
For example, in circuit C above, the input impedance equals R7, thus, 1k. If we want to amplify down to 20Hz and roll-off below that, Xc must be 1k at 20Hz, and Xc=1/(2πFC) so C=1/(2πfXc) = 8uF.
OK, let’s look at some applications now.
The Inverting Amplifier
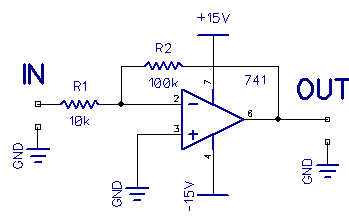
Shown above is an inverting amplifier.
If you feed 0.1V in, you get -1V out. If you feed an AC signal in, the output is 180deg out of phase with the input. The input impedance is roughly equal to R1. It will work from DC to the limit of the op-amps gain-bandwidth product. The gain is simply R2/R1, in this case, 10X. To minimize offset, we could take pin 3 to ground via a series 10k.
The Non-Inverting Amplifier
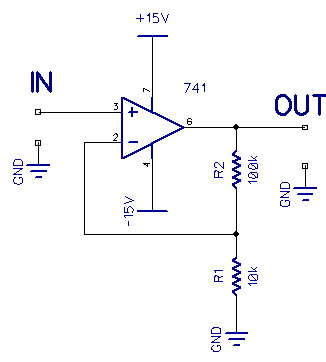
Shown above is the counterpart of the previous circuit, the non-inverting amplifier.
Here the gain is (R1+R2)/R1 or sometimes expressed as R2/R1 + 1, which is now a bit more than 10. The output is in phase with the input, but the real feature here is that the input impedance is very high, even higher if you use a FET input op-amp.
The big issue here for me with these two configurations is not to invert or invert but the input impedances. I might have a passive audio filter that I want to have precisely defined loading impedance. I could follow it with a non-inverting amplifier where the input R defines the input impedance (say 600 ohms), or I might have an active filter and want to follow it with a very high impedance so as not to load it so that I would use the non-inverting circuit.
The Voltage Follower
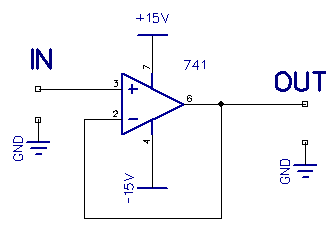
This is a special case of the non-inverting amplifier. Here, the output voltage is equal to the input voltage. You may well ask, “so, what’s the point?”
It is this: the input impedance is very high, and the output impedance is very low. This makes it most suitable as a buffer stage where you want to isolate one circuit from another, for example, in filter applications.
The Differential Amplifier
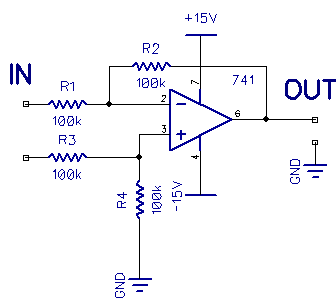
Shown above is a differential amplifier.
You might want to use this to read tiny differences across a bridge circuit, for example, in a strain gauge circuit. The voltage at one input is subtracted from the other. Here all the resistors are the same, so the gain is one. If we couple this amp with two capacitors and gave it some gain and applied it to a transducer, any signal that is present on both inputs, for example, mains hum, would be the same polarity on both pins and therefore subtracted to zero and so not present at the output.
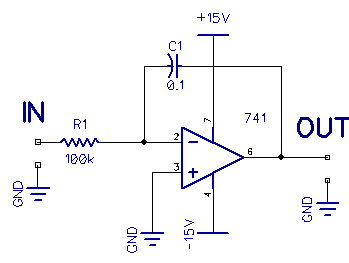
The Integrator & Differentiator
 |
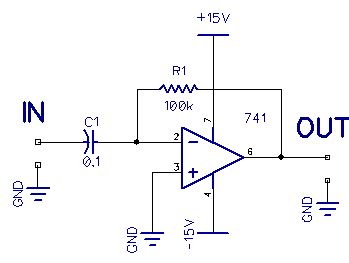 |
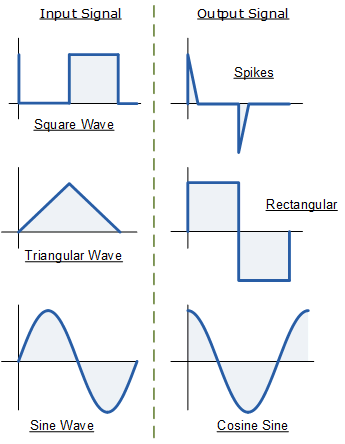
Shown on the left is an Integrator and on the right a Differentiator. Big math words, you might say, and this is true, but where would you need such a circuit?
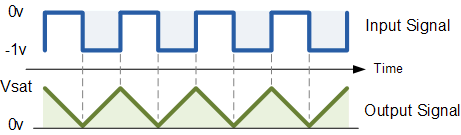
Let’s say you wanted to count acorns falling had a microphone, so every time an acorn fell, you would get a blip, and the integrator will rise to that value and keep rising and accumulating blips until you reset it. An integrator will generally have a circuit like a FET across the cap C1 to discharge it periodically. But what would happen if you fed a square wave into the integrator?
When the square wave goes high, C1 charges, and when it goes low, C1 discharges, so what you get is a triangle wave at the output.
The differentiator behaves oppositely, and without delving into the math, output waveforms show you what both circuits do.


The Summing Amplifier
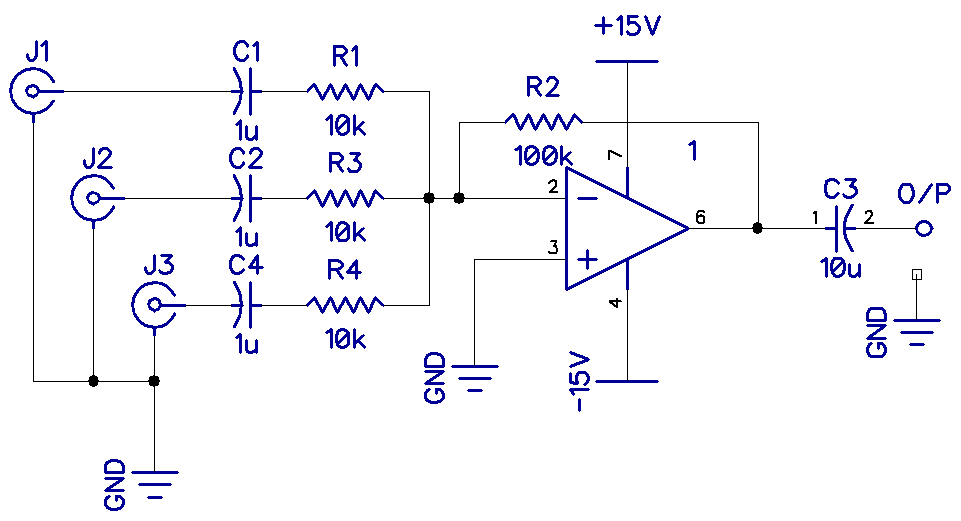

Shown above is a summing amplifier.
J1 to 3 could be a microphone, a guitar, and a keyboard. The resistors R1, 3, and 4 would be variable sliders, and the resistance of each, relative to R2, would set the level or gain. R2 could also be a pot acting like a master volume, and you would have a mixer.
Active Filters
An important use of op-amps is inactive filters. Active, meaning not made with passive components like inductors and capacitors only, but with active components to control the gain, slope, and impedances. There are 3 main types of filters, each either passing or rejecting a desired band of frequencies. The idea is to drive the input of a filter with a low impedance and then buffer its output with a high impedance. You may find several different types of each filter, each having its own pros and cons.
Four types of active filters can be made from op-amps: low-pass filter, high-pass filter, and clever series combination. These two can make a band-pass filter and a band rejects or notch filter. The design of these four filters is the subject of an article on its own (See Audio Filters article here). But shown below are some practical design examples of high and low pass filters.
| 2nd order high pass filter | 2nd order high pass filter |
  |
  |
Where R3=R4 and C1=C2 this reduces to:  |
Where R3=R4 and C1=C2 this reduces to:  |
So now, we have seen some useful linear applications of op-amps. In the next article, we will look at some non-linear applications.


