Sawtooth and Triangle Wave Generators
This is part two of the four-part tutorial series on wave generators and oscillators. But first, let’s have a recap.
What is an oscillator? It is an electronic circuit that changes the state from positive to negative in a repeating cycle without any stimulus other than DC power. This produces an AC waveform at the output. That being said, oscillators generate a repetitive waveform of the desired shape, frequency, and amplitude, usually used to drive other circuits.
Sawtooth and Triangular Oscillators
Now, let’s look at triangle and sawtooth oscillators. What is the difference between them?
A triangle wave has a symmetrical rise and fall of the waveform, but a sawtooth (also called a ramp oscillator) rises very sharply (ideally instantaneously) and then falls gradually.
Triangle waves contain an infinite number of odd harmonics, which are often used in synthesizing musical sounds. They sound like horns and trombones. They are sometimes used in switch-mode power supplies and motor control circuits. They are often used as time-base or sweep generators and in subtractive audio synthesis as the harmonics are integers and easy to work with digitally.
Sawtooth waves contain an equal amount of even and odd harmonics (unlike square waves which contain only even harmonics that’s why the sound is more musical such as guitar and fuzz box).
One of the easiest ways to generate a triangle wave is from a relaxation oscillator generating a square wave and then integrating it.
Relaxation Oscillators
Relaxation oscillators have two alternating states: a long relaxation period in which the system comes to rest and then a short change-over period in which the stable point flips over to a second stable state for a period then flips back again. The period is set by a time constant, which is usually an RC or LC pair.
Some sort of active switching device is needed, such as a transistor pair or a uni-junction transistor or an op-amp comparator, or a custom chip such as a 555. The active device switches between charging and discharging modes, producing a repeating waveform.
For any oscillator to qualify as a relaxation oscillator, it must:
- Produce a non-sinusoidal periodic waveform like triangular, square, or rectangular wave.
- The circuit of a relaxation oscillator must be nonlinear. That means the circuit design must use a semiconductor device like a transistor, MOSFET, or op-amp.
- The circuit design must use an energy-storing component like an inductor or capacitor, which charges and discharges continuously to produce a cyclic wave-form.




Seesaw A shows the seesaw in a state of equilibrium and at “relaxation,” but as the bucket slowly fills up, a tipping point is reached. The state rapidly changes as the bucket end drops and the bucket tips out. The left-hand side is suddenly much heavier and falls to the ground again and the bucket lifts and begins to fill again. In an electronic circuit, this is what happens when a capacitor gets slowly charged through a resistor until a non-linear part is reached, causing a sudden discharge, and the cycle repeats.
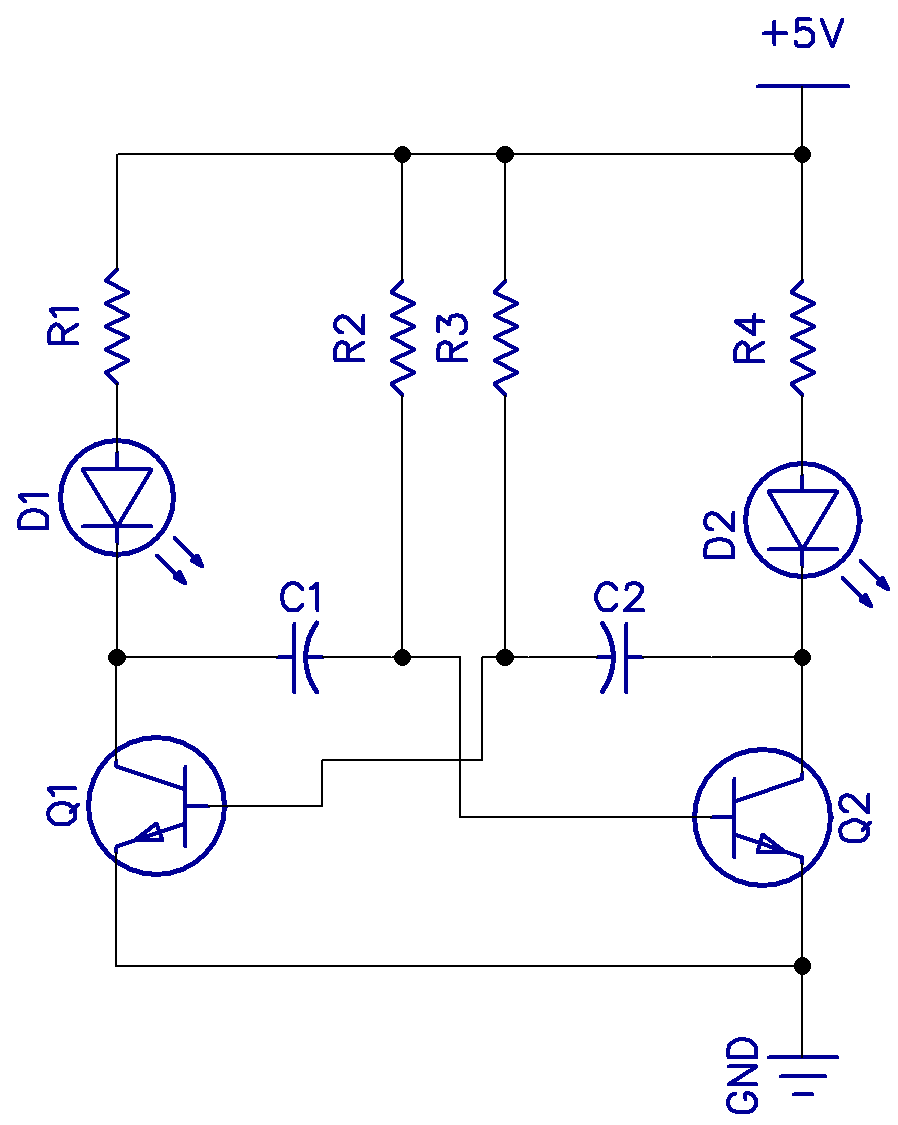

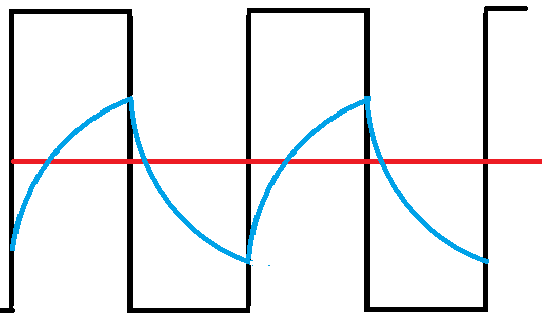

In the waveform above, the blue curve shows the voltage across one of the capacitors. It charges until the trigger point is reached, then discharges again. The black curve is the voltage at the collector, which is the square wave output. In the multivibrator, either collector can be used as the output, although in this circuit, we are just flashing two LEDs alternately.
The waveform across the capacitor looks almost like the triangle wave we are looking for, except that there is a curve to the slope as the capacitor charges and discharges. Adding a constant current source to the charge current could fix this, but there are better ways.
The easiest way to generate a triangle wave is to generate a square wave and then feed it to an integrator.
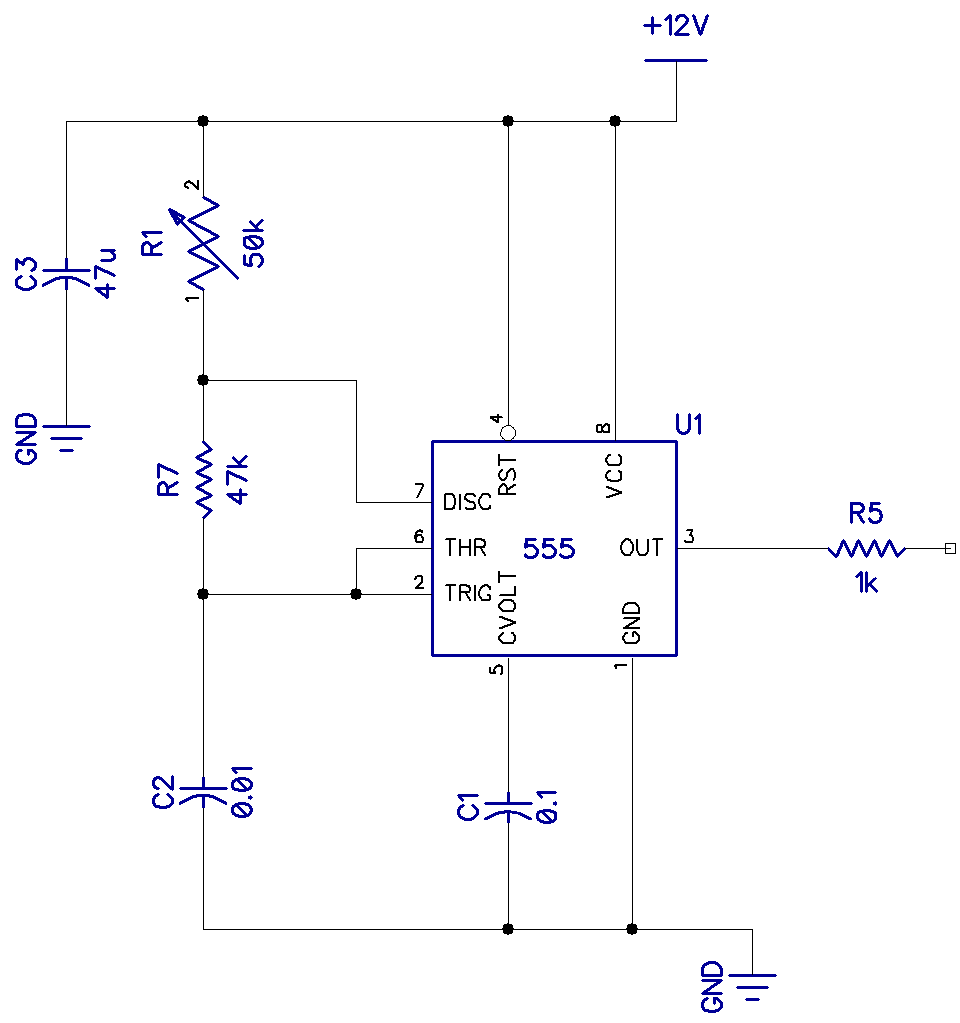

Shown above is a basic square wave oscillator using the famous 555 timer in its astable configuration. This, too, is a relaxation oscillator. R1, R7, and C2 set the frequency, and when R1 and R7 are equal, the mark-space ratio becomes almost equal.
f = 1.44/(R1+2R7)*C = 1000Hz
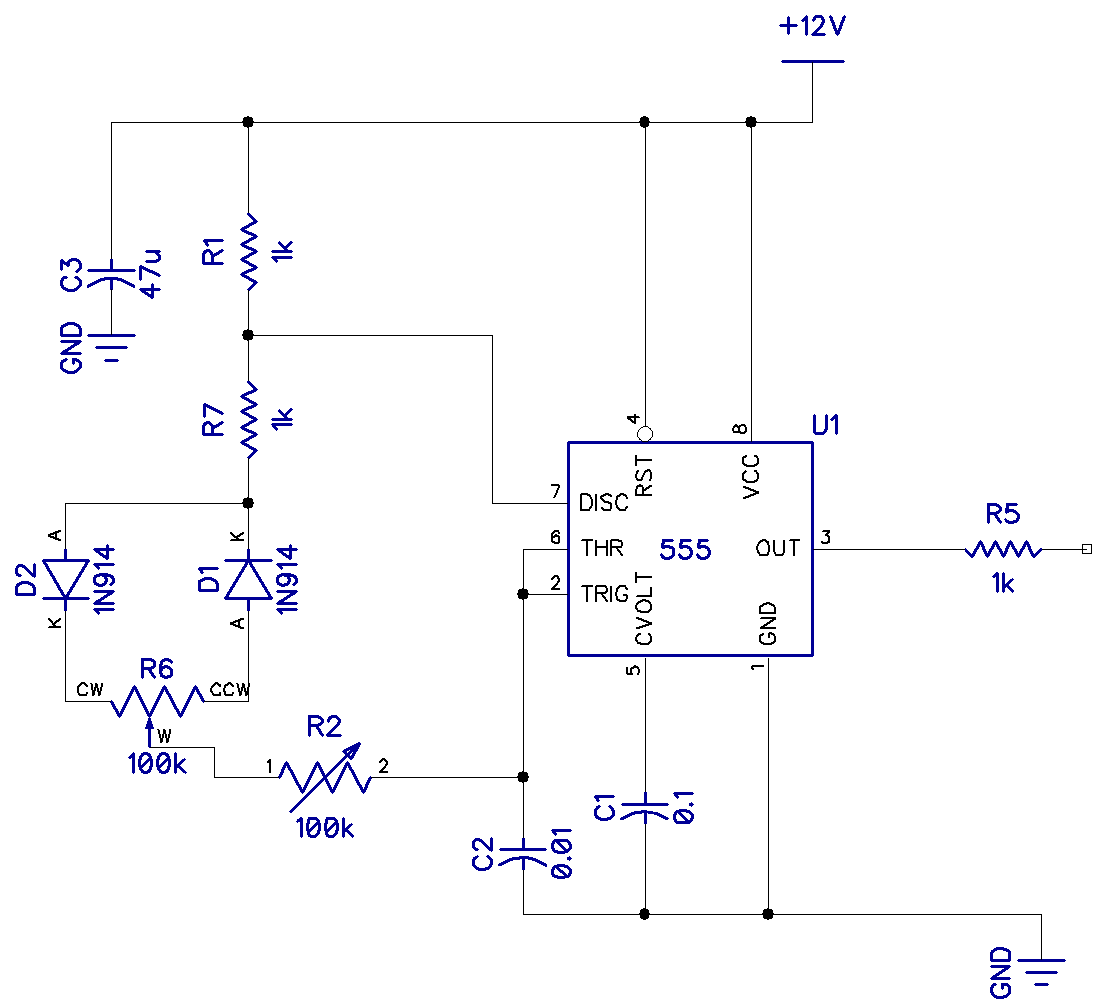
Below this, on the left side, is a modified circuit to give plenty of variation in the mark-space ratio, which we will use to perfect our triangle wave. R6 sets the mark-space ratio and R2 sets the frequency. By careful adjustment of the mark-space ratio, the time constants on the rising and falling slopes of the triangle waveform of the integrator can be made perfectly symmetrical.
On the right is the integrator. The output of the square wave oscillator is fed into pin 2 of the integrator which converts the square wave into a triangle wave. C3 removes any sharp edge transitions while R3 provides some DC feedback for stability.
  |
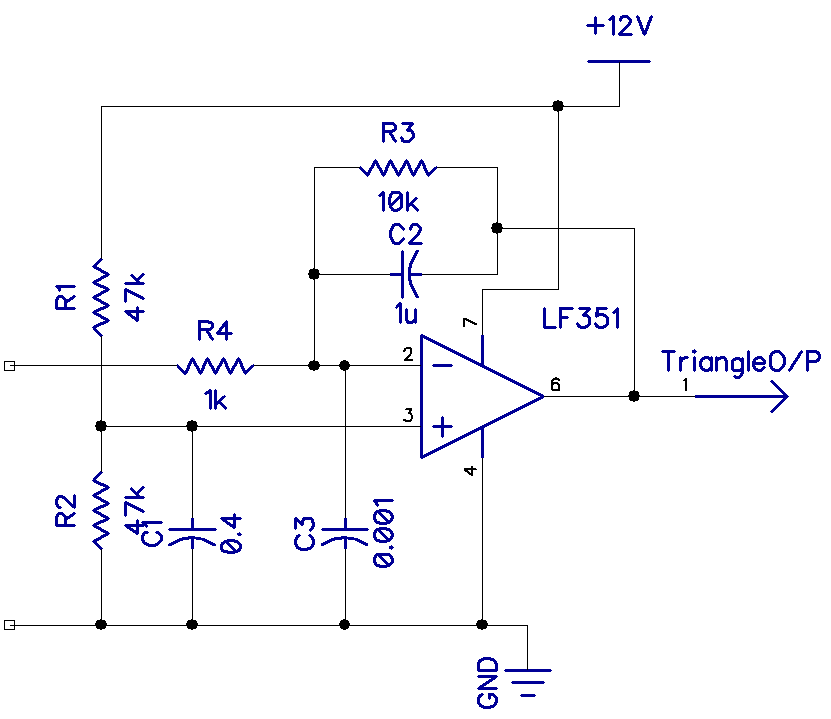  |
| 555 with an adjustable mark-space ratio | Op-amp integrator |
  |
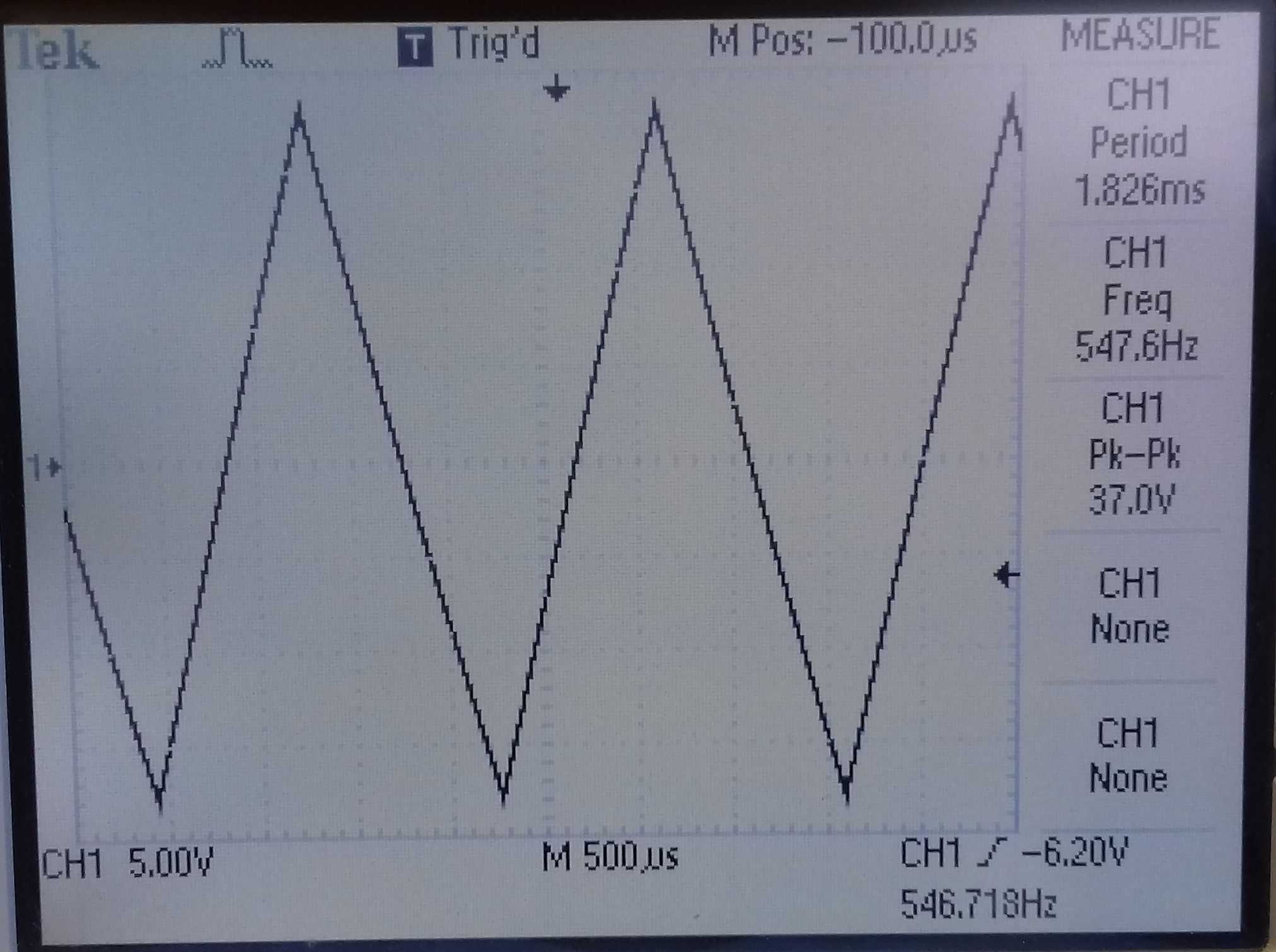  |
| Breadboard of variable mark-space and integrator | Output waveform |
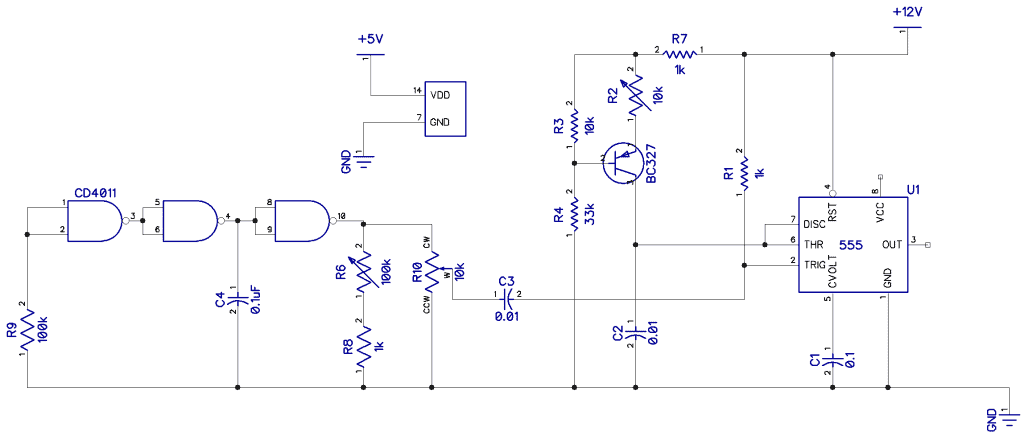
Generating a sawtooth or ramp is a little trickier if you want the rise time to be practically zero and a clean linear slope to the fall. The circuit below features the identical CMOS 4011 square wave oscillator we used in part 1 (square wave oscillators). The square wave output is fed into the trigger input of a 555 configured as a monostable, which fires every time a low going pulse is received at pin 2 (trigger). The charge rate is now controlled by a constant current source (BC237) to linearise the slope of the ramp (we mentioned this earlier).
Shown below is a breadboard of the monostable and the very fine resulting waveform. The frequency is, of course, a function of the square wave generator and is 1/(2.2R6*C4).

  |
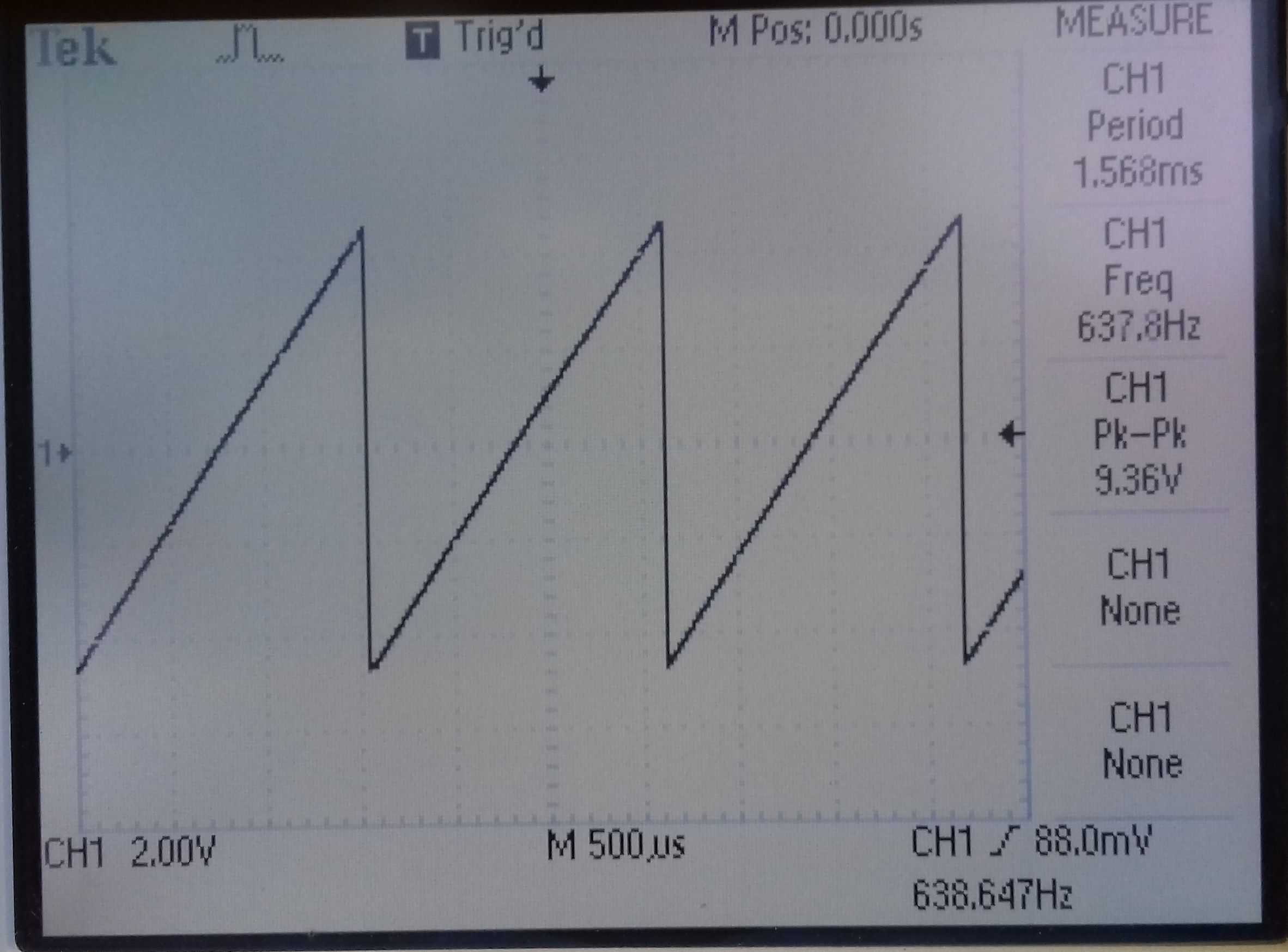  |
| Breadboard of sawtooth oscillator | Output waveform |
There you go! For part 3, we will look at sine wave oscillators.


